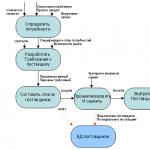
Прямолинейное равномерное движение. Типы движений Проекция ускорения движущегося тела на ось ox

Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.

Векторы начальной скорости и ускорения могут иметь различные направления, поэтому переход от векторной записи уравнений к алгебраической может оказаться весьма трудоемким.

Известно, что проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось.

График скорости

Из уравнения следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось OX равна нулю, то прямая проходит через начало координат.

Основные виды движения

1. а n = 0, a t = 0 – прямолинейное равномерное движение;

2. а n = 0, a t = const – прямолинейное равнопеременное движение;

3. а n = 0, a t ¹ 0 – прямолинейное с переменным ускорением;

4. а n = const, a t = 0 – равномерное по окружности

5. а n = const, a t = const – равнопеременное по окружности

6. а n ¹ const, a t ¹ const – криволинейное с переменным ускорением.

Вращательное движение твердого тела.

Вращательное движение твердого тела относительно неподвижной оси – движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.

Равномерное движение по окружности

Рассмотрим наиболее простой вид вращательного движения, и уделим особое внимание центростремительному ускорению.

При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения.

Из подобия треугольников OAB и BCD следует

Если интервал времени ∆t мал, то мал и угол a. При малых значениях угла a длина хорды AB примерно равна длине дуги AB, т.е. . Т.к. , , то получаем

Поскольку , то получаем

Период и частота

Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодам обращения (Т ). Т.к. длина окружности равна 2pR , период обращения при равномерном движении тела со скоростью v по окружности радиусом R равняется:

Величина, обратная периоду обращения, называется частотой. Частота показывает, сколько оборотов по окружности совершает тело в единицу времени:

(с -1)

Кинематика вращательного движения

Для указания направления вращения малым углам поворота приписывают направление: направлен по оси вращения так, чтобы рассматриваемое с его конца вращение происходило против часовой стрелки (правило правого винта). Если тело сделало N поворотов: . Средняя угловая скорость:

Мгновенная угловая скорость:

(12)

Графики дают возможность представить зависимость скорости и ускорения от времени при движении тела (точки) наглядно.
Графики модуля и проекции ускорения
Если точка движется с постоянным ускорением, то графики модуля и проекции ускорения будут прямыми, параллельными оси времени. Надо помнить, что модуль - неотрицательная величина, поэтому график модуля ускорения не может быть расположен ниже оси времени (рис. 1.50). Проекции ускорения могут иметь положительные и отрицательные значения (рис. 1.51, а, б). Рисунок 1.51, б показывает, что ускорение постоянно и направлено противоположно оси X.
Рис. 1.50

о
По графику проекции ускорения можно найти, кроме ах, изменение проекции скорости. Оно численно равно площади пря-моугольника ОАВС или OKMN, так как Avx = axt, a axt численно равно площади прямоугольника ОАВС или OKMN.
Площадь берется со знаком минус, если она расположена ниже оси времени, что соответствует рисунку 1.51, б, где Avx = axt
Формулы проекций скорости (1.17.3) являются линейными функциями времени. Поэтому графики модуля и проекций ско-рости представляют собой прямые линии. На рисунке 1.52 пред-ставлены графики зависимости модуля скорости от времени для трех движений с постоянным ускорением. Графики 2 и 3 соот-ветствуют движениям, модули начальных скоростей которых соответствуют отрезкам OA и ОБ. График 1 соответствует движению с равномерно возрастающим модулем скорости и начальной скоростью, равной нулю. График 3 соответствует движению с модулем скорости, равномерно убывающим до ну-ля. Отрезок ОС численно равен времени движения точки до ос-тановки. Рис. 1.52
График проекции скорости
Графики модуля скорости содер- /1
о
жат меньше информации, чем графики проекции скорости, так как по первым графикам нельзя судить о направлении движения относительно координатных осей.
Рис. 1.53
На рисунке 1.53 изображены графики 1, 2 проекций скорости двух точек. Обе они имеют начальную скорость, равную нулю. Первая точка движется в
положительном направлении оси X, и так как Avx > 0, то а1х > 0. Вторая точка движется противоположно оси X, так как Avx На рисунке 1.54 также изображены графики 1, 2 проекций скорости двух точек. Обе они имеют одно и то же значение проекции начальной скорости, соответствующее отрезку OA. Согласно графику 1 точка движется в положительном направлении оси X, причем модуль и проекция скорости равномерно возрастают.
Согласно графику 2 (см. рис. 1.54) точка в течение некоторого промежутка времени (отрезок ОВ) движется в положительном направлении оси X (vx > 0) с равномерно уменьшающимся до нуля (остановка) значением проекции скорости. После этого проекция скорости становится отрицательной; это означает, что точка стала двигаться в направлении, противоположном положительному направлению оси X. При этом проекция скорости по модулю, а значит, и модуль скорости равномерно увеличиваются. Проекция ускорения точки отрицательна. Так как проекция скорости точки равномерно убывает, то проекция ускорения остается постоянной. Следовательно, точка движется с постоянным ускорением.
Графики зависимости скорости и ускорения от времени при постоянном ускорении довольно просты. Глав-ное здесь - привыкнуть к изображению положительных и отрицательных величин и не путать графики модулей и проекций.
? 1. Покажите, что угол наклона графика проекции скорости к оси времени тем больше, чем больше модуль проекции ускорения, т. е. проекция ускорения является угловым коэффициентом прямой.
2. На рисунке 1.55 изображены графики 1, 2 проекций скорости двух точек. Докажите, что графики соответствуют движению с ускорением, не изменяющимся как по модулю, так и по направлению.? Рис. 1.54 Рис. 1.55
Как изменяется скорость точки, график проекции скорости которой в зависимости от времени изображен прямой 1 (см. рис. 1.55)? Чему соответствуют отрезки ОС и ОХ>?
Как изменялась скорость точки (см. график 2 на рисунке 1.55)? Чему соответствует отрезок ОС? Куда направлено ускорение точки относительно оси XI

Скорость является одной из основных характеристик . Она выражает саму суть движения, т.е. определяет то отличие, которое имеется между телом неподвижным и телом движущимся.

Единицей измерения скорости в системе СИ является м/с .

Важно помнить, что скорость – величина векторная. Направление вектора скорости определяется по движения. Вектор скорости всегда направлен по касательной к траектории в той точке, через которую проходит движущееся тело (рис.1).

К примеру, рассмотрим колесо движущегося автомобиля. Колесо вращается и все точки колеса движутся по окружностям. Брызги, разлетающиеся от колеса, будут лететь по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек колеса.

Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и быстроту его перемещения (модуль вектора скорости).

Отрицательная скорость

Может ли скорость тела быть отрицательной? Да, может. Если скорость тела отрицательна, это значит, что тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. На рис.2 изображено движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Следует помнить, что говоря о знаке скорости, мы имеем ввиду проекцию вектора скорости на координатную ось.

Равномерное и неравномерно движение

В общем случае скорость зависит от времени. По характеру зависимости скорости от времени, движение бывает равномерное и неравномерно.

ОПРЕДЕЛЕНИЕ

Равномерное движение – это движение с постоянной по модулю скоростью.

В случае неравномерного движения говорят о :

Примеры решения задач по теме «Скорость»

ПРИМЕР 1

Задание	Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля.
Решение	Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. Воспользуемся определением средней скорости: Так как предполагается прямолинейное равномерное движение, знаки векторов можно опустить. Время, потраченное автомобилем на прохождение всего отрезка пути: где — время, затраченное на прохождение первой половины пути, а — время, затраченное на прохождение второй половины пути. Суммарное перемещение равно расстоянию между населенными пунктами, т.е. . Подставив эти соотношения в формулу для средней скорости, получим: Переведем скорости на отдельных участках в систему СИ: Тогда средняя скорость автомобиля: (м/с)
Ответ	Средняя скорость автомобиля равна 18,8 м/с

ПРИМЕР 2

Задание	Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 25 м/с. Определить среднюю скорость автомобиля.
Решение	Сделаем рисунок.

На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.

Проекция точки

Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.

Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.

Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.

Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.

Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).

Как найти длину проекции

Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).

Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.

Проекция скорости

Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.

Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.

Проекция вектора

При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот.

Возьмем следующее координатное уравнение: x = x(t), y = y(t), z = z(t). В данном случае функция скорости будет спроецирована на три оси и будет иметь следующий вид: V(x) = dx / dt = x"(t), V(y) = dy / dt = y"(t), V(z) = dz / dt = z"(t). Отсюда следует, что для нахождения скорости необходимо брать производные. Сам же вектор скорости выражается уравнением такого вида: V = V(x) i + V(y) j + V(z) k. Здесь i, j, k являются единичными векторами координатных осей x, y, z соответственно. Таким образом, модуль скорости вычисляется по следующей формуле: V = √ (V(x) ^ 2 + V(y) ^ 2 + V(z) ^ 2).

Определение

Равномерное прямолинейное движение -- это движение с постоянной скоростью, при котором ускорение отсутствует, а траектория движения представляет собой прямую линию.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена так же, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости: $\left\langle v\right\rangle =v$

Определение

Скорость равномерного прямолинейного движения -- это физическая векторная величина, равная отношению перемещения тела $\overrightarrow{S}$ за любой промежуток времени к значению этого промежутка t:

$$\overrightarrow{v}=\frac{\overrightarrow{S}}{t}$$

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

$$ \overrightarrow{S} = \overrightarrow{v} \cdot t $$

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна: $v_x = v$, то есть $v $>$ 0$

Проекция перемещения на ось ОХ равна: $s = v_t = x - x0$

где $x_0$ - начальная координата тела, $х$ - конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени $х = х(t)$, принимает вид: $х = x_0 + v_t$

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля ($v $

Зависимость проекции скорости тела от времени показана на рис. 1. Так как скорость постоянна ($v = const$), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 2), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 2. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 3. Из графика видно, что проекция скорости на ось Ot численно равна тангенсу угла наклона графика к оси времени:

Рис. 3. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 4. Из рисунка видно, что

tg $\alpha $1 $>$ tg $\alpha $2, следовательно, скорость тела 1 выше скорости тела 2 (v1 $>$ v2).

tg $\alpha $3 = v3 $

Рис. 4. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть х = х0

Задача 1

Два поезда движутся на встречу друг другу по параллельным рельсам. Скорость первого поезда 10 метров в секунду, длина первого поезда 500 метров. Скорость второго поезда 30 метров в секунду, длина второго поезда 300 метров. Определить в течение какого времени второй поезд будет ехать мимо первого.

Дано: $v_1$=10 м/с; $v_2$=30 м/с; $L_1$=500 м; $L_2$=300 м

Найти: t --- ?

Время, в течение которого поезда будут проходить мимо друг друга, можно определить, разделив общую длину поездов на их относительную скорость. Скорость первого поезда относительно второго определяется по формуле v= v1+v2 Тогда формула для определения времени принимает вид: $t=\frac{L_1+L_2}{v_1+v_2}=\frac{500+300}{10+30}=20\ c$

Ответ: второй поезд будет ехать мимо первого в течение 20 секунд.

Задача 2

Определить скорость течения реки и скорость катера в стоячей воде, если известно, что катер проходит расстояние 300 километров по течению за 4 часа, а против течения -- за 6 часов.

Дано: $L$=300000 м; $t_1$=14400 с; $t_2$=21600 с

Найти: $v_p$ - ?; $v_k$ - ?

Скорость катера по течению реки относительно берега $v_1=v_k+v_p$, а против течения $v_2=v_k-v_p$ . Запишем закон движения для обоих случаев:

Решив уравнения относительно vp и vk, получаем формулы для расчета скорости течения реки и скорости катера.

Скорость течения реки: $v_p=\frac{L\left(t_2-t_1\right)}{2t_1t_2}=\frac{300000\left(21600-14400\right)}{2\times 14400\times 21600}=3,47\ м/с$

Скорость катера: $v_к=\frac{L\left(t_2+t_1\right)}{2t_1t_2}=\frac{300000\left(21600+14400\right)}{2\times 14400\times 21600}=17,36\ м/с$

Ответ: скорость течения реки равна 3,47 метров в секунду, скорость катера равна 17,36 метров в секунду.