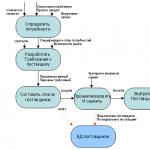
На каждый день. Прямая задача в плоском напряженном состоянии

Круг Мора - это круговая диаграмма, дающая наглядное представление о напряжениях в различных сечениях, проходящих через данную точку. Названа в честь Отто Кристиана Мора . Является двумерной графической интерпретацией тензора напряжений .

Первым человеком, создавшим графическое представление напряжений для продольных и поперечных напряжений изгибаемой горизонтальной балки был Карл Кульман . Вклад Мора заключается в использовании этого подхода для плоского и объёмного напряжённых состояний и определение критерия прочности , основанного на круговой диаграмме напряжений .

Энциклопедичный YouTube

1 / 5
Внутренние усилия возникают между частицами сплошного деформируемого тела в качестве реакции на прикладываемые внешние силы: поверхностные и объёмные . Эта реакция согласуется со вторым законом Ньютона , приложенным к частицам материальных объектов. Величина интенсивности этих внутренних сил называется механическим напряжением . Т.к. тело считается сплошным, эти внутренние силы распределяются непрерывно по всему объёму рассматриваемого объекта.
cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2 , sin 2 ⁡ θ = 1 − cos ⁡ 2 θ 2 , sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ {\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}},\qquad \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}\qquad {\text{,}}\qquad \sin 2\theta =2\sin \theta \cos \theta }
Тогда можно получить
σ n = 1 2 (σ x + σ y) + 1 2 (σ x − σ y) cos ⁡ 2 θ + τ x y sin ⁡ 2 θ {\displaystyle \sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta }
Касательное напряжение также действует на площадке площадью d A {\displaystyle dA} . Из равенства проекций сил на ось τ n {\displaystyle \tau _{\mathrm {n} }} (ось y ′ {\displaystyle y"} ) получаем:
∑ F y ′ = τ n d A + σ x d A cos ⁡ θ sin ⁡ θ − σ y d A sin ⁡ θ cos ⁡ θ − τ x y d A cos 2 ⁡ θ + τ x y d A sin 2 ⁡ θ = 0 τ n = − (σ x − σ y) sin ⁡ θ cos ⁡ θ + τ x y (cos 2 ⁡ θ − sin 2 ⁡ θ) {\displaystyle \ {\begin{aligned}\sum F_{y"}&=\tau _{\mathrm {n} }dA+\sigma _{x}dA\cos \theta \sin \theta -\sigma _{y}dA\sin \theta \cos \theta -\tau _{xy}dA\cos ^{2}\theta +\tau _{xy}dA\sin ^{2}\theta =0\\\tau _{\mathrm {n} }&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta +\tau _{xy}\left(\cos ^{2}\theta -\sin ^{2}\theta \right)\\\end{aligned}}}
Известно, что
cos 2 ⁡ θ − sin 2 ⁡ θ = cos ⁡ 2 θ , sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ {\displaystyle \cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta \qquad {\text{,}}\qquad \sin 2\theta =2\sin \theta \cos \theta }
Тогда можно получить
τ n = − 1 2 (σ x − σ y) sin ⁡ 2 θ + τ x y cos ⁡ 2 θ {\displaystyle \tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta }
Круги мора - круговые диаграммы, дающие наглядное представление о напряжениях в разных сечениях, проходящих через данную точку. В системе координат τ n - σ n - три (полу)окружности, которых по оси абсцисс являются разностью главных нормальных напряжений σ 1 , σ 2 , σ 3 (рис.). Максимальная окружность радиусом (σ 1 -σ 3)/2 охватывает две внутренние окружности радиусами (σ 1 -σ 2)/2 и (σ 2 -σ 3)/2, касающихся в точке σ 2 . Координаты точек в пространстве между дугами этих окружностей - нормальные и касательные в произвольно ориентированных площадках. На осях окружностей находятся соответственно . Положение точки σ 2 определяется коэффициентом Лоде - Надаи. Аналогично кругам Мора в координатах γ - ε строят для исследования деформированного состояния, где R 1 = (ε 2 -ε 1)/2 = 0,5γ 23 , R 2 = (ε 1 -ε 3)/2 = 0,5γ 31 , R 3 = (ε 1 -ε 2)/2 = 0,5γ 12
Круги Мора (круговая напряжений)
Энциклопедический словарь по металлургии. - М.: Интермет Инжиниринг . Главный редактор Н.П. Лякишев . 2000 .

Смотреть что такое "Круги мора" в других словарях:
Круг Мора (рис. 8.2 ) вычерчивается в прямоугольной системе координат. Полагается, что σ 1 ≥σ 2

Рис. 8.2. Графическое представление напряженного состояния грунта (круг Мора)

Построение круга Мора производится в следующей последовательности. От начала координат откладываем значения σ 1 и σ 3 . Из точки В проводят окружность радиусомт R . Любая точка E на окружности характеризует напряженное состояние грунта в плоскости, проходящей через рассматриваемую точку. Угол наклона α линии ЕА - это угол наклона рассматриваемой площадки к главной. Центральный угол наклона отрезка EB равен 2α. Нормальные напряжения по этой площадке а представляются по горизонтальной оси отрезком ОЕ", касательные τ - перпендикулярным отрезком ЕЕ" .

Значения σ и τ могут быть определены через σ 1 и σ 3 по формулам (8.1) и (8.2).

Максимальные и минимальные касательные напряжения соответствуют sin 2α = 1 и sin 2α = -1, т.е. углам 2α=π/2 или 3π/2 (α=45° или 135°).

Полное результирующее напряжение на рассматриваемой площадке

Угол отклонения σ n от нормали к площадке

(8.4)

Значение угла θ при изменении угла α от 0 до 90° сначала возрастает от нуля до некоторого θ max , а затем убывает до нуля.

Угол θ максимален, когда линия ОE станет касательной к кругу напряжений. Из треугольника ОBЕ :

(8.5)

Максимальное отклонение полного (результирующего) напряжения на угол θmax нормали к площадке имеет место при:

Следовательно, отклонения площадки скольжения от направления наибольшего главного напряжения σ 1

(8.7)

Таким образом, в предельном состоянии в каждой точке грунта имеются две сопряженные площадки скольжения, наклоненные под углом 45°- φ/2 к линии действия максимального и 45° + φ/2 - минимального главного напряжения (рис. 8.3 ).

Рис. 8.3. Ориентация площадок скольжения относительно главных напряжений: 1, 2 - площадки скольжения

Для сыпучих грунтов во всех случаях θ max не может быть больше угла внутреннего трения φ. А разрушение сыпучих грунтов наступает, когда угол отклонения полного(результирующего) напряжения равен углу внутреннего трения:

θ max = φ (8.8)

Выражение (8.8) является условием прочности грунта. Тогда уравнение предельного равновесия можно записать в следующем виде:

(8.9)

Выражение (8.9) известно в механике грунтов как условие прочности (предельного равновесия) для песчаных (сыпучих) грунтов. После несложных тригонометрических преобразований это выражение можно записать в следующем виде:

(8.10)

(8.11)

Это выражение часто используют в теории давления грунтов на ограждения (глава 10). Для связных грунтов также можно записать условие предельного равновесия, предварительно построив круги Мора (рис. 8.4 ) по результатам испытания в стабилометре (см. рис. 5.7).

Рис. 8.4. Круги Мора, построенные по результатам испытания образцов грунта на сжатие в стабилометре

Радиус круга

ВД = (σ 1 - σ 3)/2 (8.12)

а отрезок О"Д можно найти из выражения

Отрезок О"О , отсекаемый наклонной линией на оси абсцисс (см. рис. 8.4), называют давлением связности, которое можно представить в виде

(8.14)

Давление связности (8.14) можно условно считать начальным давлением связного грунта, которое необходимо преодолеть при испытании на сдвиг. Зная ВД (8.12) и О"Д (8.13), а также используя (8.14), найдем

(8.15)

Выражение (8.15), связывающее главные напряжения в момент разрушения образца с углом внутреннего трения, принято называть уравнением предельного равновесия для связных грунтов.

Уравнение (8.15) в некоторых случаях удобно использовать не в главных напряжениях, а в компонентах, записанных относительно координатных осей. Из сопротивления материалов известно, что:

(8.16)

Тогда, рассматривая совместно уравнения (8.15) и (8.16), можно записать уравнение предельного равновесия в следующем виде:

(8.17)

Аналогичным образом можно выразить и уравнение (8.9).

Зависимость напряжений σ n и τ n , действующих на площадку с нормалью n, проходящую через рассматриваемую точку, можно представить наглядно графически при помощи круговой диаграммы Мора (кругов Мора).

ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ . Заданы главные напряжения σ 1 и σ 2 (см. рис. 2) . Откладываются отрезки ОA=σ 1 и ОВ=σ 2 с учетом знаков (рис. 1). На отрезке АВ, как на диаметре, строится окружность. Из точки В проводится прямая под углом α к оси σ. Координаты точки D пересечения этой прямой с окружностью дают напряжения по наклонной площадке: ОЕ=σ n , ED=τ n .

Рисунок 1.

Заданы напряжения α х, σ y , τ ху (рис. 2). Откладываются отрезки ОЕ=σ х и OF=σ y с учетом знаков. Из точки Е (независимо от ее положения) откладывается отрезок ED=τ xy также с учетом знака. Из точки С, делящей отрезок EF пополам, как из центра строится окружность радиусом CD. Прямая BD определяет направление действия вектора главного напряжения σ 1 , а абсциссы точек пересечения окружности с осью σ дают величины главных напряжений: OА=σ 1 , ОВ=σ 2 .

Рисунок 2.

ОБЪЕМНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ . Строятся три полуокружности на отрезках, изображающих разности главных напряжений σ 1 -σ 3 , σ 2 -σ 3 , σ 1 -σ 2 , как на диаметрах (рис. 3). Напряжения σ n и τ n по наклонной площадке, нормаль к которой образует углы α, β и γ с направлениями трех главных напряжений, определяются путем следующего построения. Проводятся линии АЕ и BF соответственно под углами α и γ от вертикали. Через полученные точки пересечения Е и F проводятся дуги радиусами С 2 Е и C 1 F до пересечения в точке D, координаты которой и дают величины напряжений σ n и τ n . Точки, изображающие напряженные состояния по разным площадкам, не выходят из области, заключенной между тремя полуокружностями (заштрихована на рисунке).

Известным немецким ученым Мором был предложен графический метод определение напряжений σ α и τ α при заданных σ 1 ,σ 2 и α в случае плоского напряженного состояния.

Рис.18.1. Случай плоского напряженного состояния.

Для этого выбирается плоская система координат, при этом оси абсцисс соответствуют нормальные напряжения, а оси ординат – касательные напряжения

По оси абсцисс откладывают напряжения σ 1 =ОА и σ 2 =ОВ

На разнице отрезков ОА - ОВ = σ1 - σ2 , радиусом ВС = (σ1 - σ2)/2 строится круг. откладывая от оси абсцисс против часовой стрелки угол 2α, получаем на круге точку D и опускаем из нее на ось абсцисс перпендикуляр – DK

Полученный отрезок ОК = σ α , а отрезок DК = τ α

Круги Мора позволяют анализировать все виды напряженного состояния тела.

Рис.18.2. Графическое определение напряжений. Круг Мора.

Задача.

Определить аналитически и с помощью круга Мора нормальное σα и касательное τα напряжения в сечении АВ, расположенном под углом β=60º к продольной оси. Стержень растягивается силой Р =20кН, площадь его поперечного сечения равна 200*200мм2, α = 90- β

Находим главное напряжение

т.к. рассматривается случай линейного напряженного состояния

Для графического определения напряжений выбираем систему координат σ – τ. По оси σ откладываем в выбранном масштабе напряжение σ 1 в виде отрезка ОМ, который делим пополам, и отрезком очерчиваем круг. Из точки М (полюс круга Мора) проводим прямую параллельную АВ или параллельную нормали к АВ. Получаем точку D пересечения прямой с кругом. Абсцисса ОD1 будет представлять σ α =37МПа, а ордината DD1 - τ α =21,5МПа.

ОБОБЩЕННЫЙ ЗАКОН ГУКА В ОБЩЕМ СЛУЧАЕ НАПРЯЖЕННОГО СОСТОЯНИЯ.

При исследовании деформаций в случае объемного напряженного состояния предполагается, что материал подчиняется закону Гука и что деформации малы.

Рассмотрим элемент, размеры граней которого равны а*в*с и по этим граням действуют главные напряжения σ 1 ,σ 2 ,σ 3.

Все напряжения считаем положительными. Вследствие деформации ребра элемента изменяют свою длину и становятся равными а+∆а, в+∆в, с+∆с. Отношения приращений длины ребер элементов к их первоначальной их длине дадут главные относительные удлинения в главных направлениях:

Под действием напряжения σ 1 ребро длиной а получит относительное удлинение

Напряжения σ 2 и σ 3 действуют поперек ребра а, поэтому они будут препятствовать его удлинению. Деформации, вызванные действием σ 2 , σ 3 в направлении ребра а будут равны.
Рекомендуем также

Loading...